
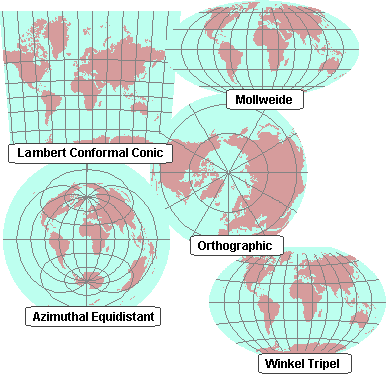
IMAGE CONVERT BETWEEN MAP PROJECTIONS FULL
While planar coordinates are helpful to calculate the relative distance between objects or areas, they are often not meaning full to the average user. Geographic (spherical) coordinates are converted to projected (planar) coordinates based on the definition of the projection. Usually the origin is shifted in such a way that all planar coordinates within the map extent are positive.Īll planar projections always have an underlying geographic projection, based on a datum ( see a good explanation here ). The location of the origin (0,0 coordinate ) may vary for different projections and is defined by the false easting and false northing value. If you use a planar projection such as mercator, mapping unit is usually in meter (eg UTM) in some cases in feet. If so, is it based on the class of projection (planar, cylindrical, conic), or specific to the individual projection? Snyder lays out rectangular coordinates in tables in his manual, but they don't seem to correlate with each other.Ĭoordinate system for different projection are usually in the mapping unit of the projection. It seems my mistake is that, in the algorithm I laid out above, the projected space is always a pixel coordinate system.Īm I correct to understand that each map projection has its own rectangular coordinate system? That is, Mercator rectangular coordinates mean something different than Gnomonic rectangular coordinates, etc. I have been trying to follow these steps for converting between an equirectangular map and various projections. (4) Sample according to the output of step (3) in order to render the new image. (3) Apply the forward projection to the normalized coordinates of that grid to determine where in the original image to sample (2) Find the min/max bounds of that projection and create a grid in that space (1) Apply the inverse projection to the normalized pixel coordinates of the image "undistorting" an image, which is kind of like an inverse projection of some image distortion), the standard algorithm is: When resampling an image according to some function (e.g. I hope it may be more clear if I explain how I have arrived at my confusion.
IMAGE CONVERT BETWEEN MAP PROJECTIONS HOW TO
Where I am struggling is how to go from that arbitrary scale to my pixel grid. I've been reading through Snyder's " Map Projections: A Working Manual" and I think I've concluded that the rectangular coordinates output from the forward projections are arbitrary in scale. Here it's called the reference transformation. I think it illustrates the step I am confused about. I found the image below on slide 60 of this powerpoint.
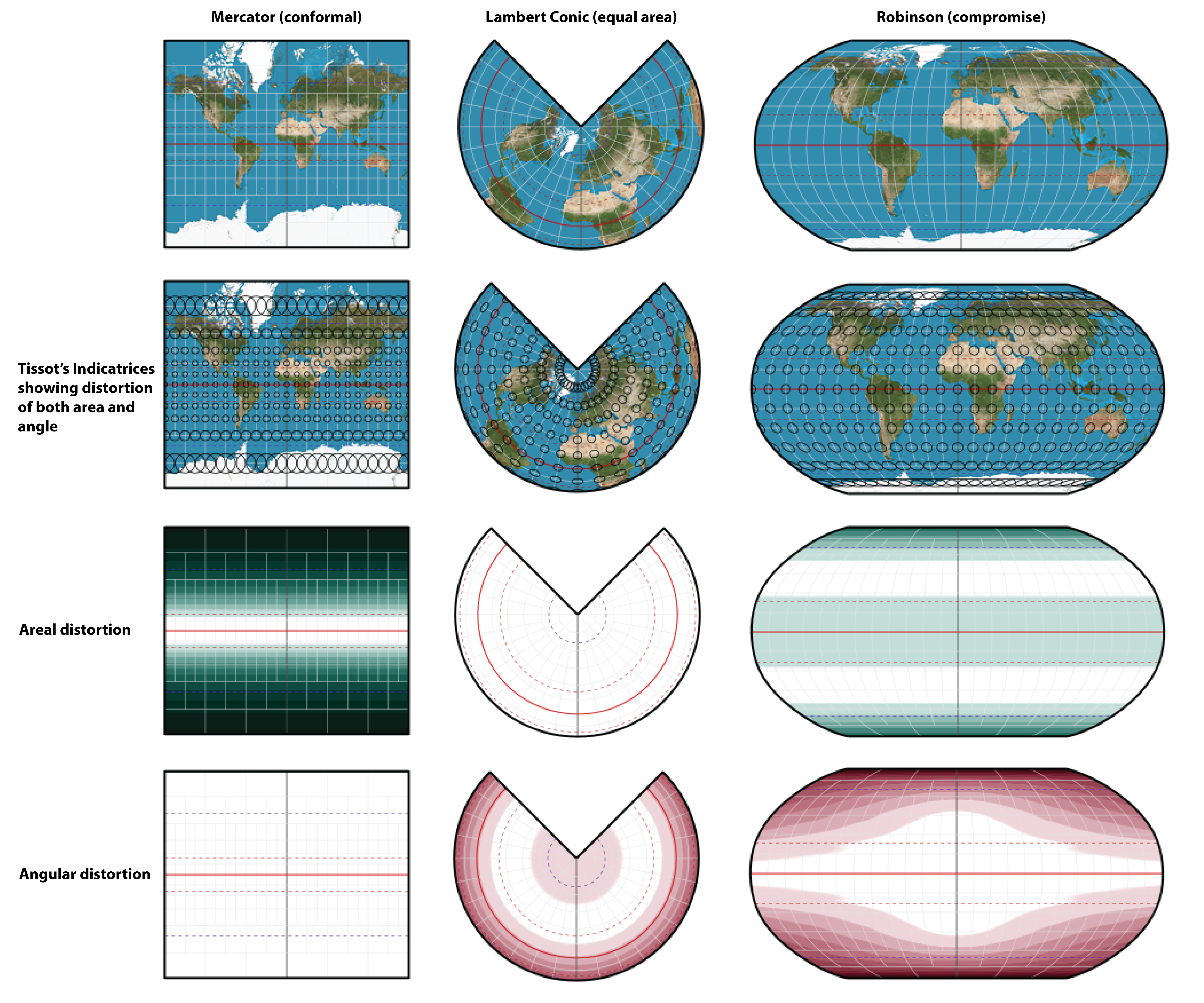

Perhaps this additional info may help to explain my confusion. the map) if they're still in spherical coordinates? In my case, I ultimately need to identify actual pixel locations when I render the new projections, but generally speaking it is not clear to me what these spherical (x,y) values mean with regard to the mapping surface. How do these (x,y) values translate to actual locations on the tangent plane (i.e. I get that (x,y) represent locations on the tangent plane, except that they are still in spherical coordinates: e.g. Take the Mercator projection, for example. The thing that I still don't quite understand is how to interpret the (x,y) values of the projection. I have been playing around with a variety of map projections for the purposes of transforming between various representations.


 0 kommentar(er)
0 kommentar(er)
